MATRICES ESPECIALES

 

Matriz Identidad

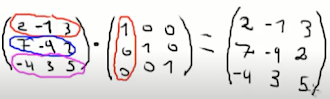
Es una matriz tal que al multiplicar cualquier matriz ya sea desde la derecha o desde la izquierda por la matriz identidad obtenemos la misma matriz. (Una matriz identidad es cuadrada). Una matriz identidad es aquella que su diagonal principal se conforma de solo números (1) y el número (0) abarca el resto de las posiciones.

Ejemplo:

Matriz Diagonal

Se define como matriz diagonal cuando todos los elementos de una matriz “cuadrada” son iguales a 0 excepto los números que se encuentran en su diagonal principal. Los elementos de la diagonal principal pueden ser distintos de 0.

Ejemplo:

Matriz triangular superior:

Es una matriz cuadrada que tiene un triángulo de ceros por debajo de la diagonal principal

Ejemplo:

Matriz triangular inferior

Es una matriz cuadrada que tiene un triángulo de ceros por encima de la diagonal principal.

Ejemplo:

Matriz Traspuesta:

la matriz traspuesta es aquella que surge como resultado de realizar un cambio de columnas por filas y filas por columnas en la matriz original, generándose una nueva matriz (a la que llamamos traspuesta).

Ejemplo:

Matriz Simétrica:

Una matriz AA es simétrica si es igual a su traspuesta, es decir, A=ATA=AT. Como consecuencia de la definición, la matriz AA tiene que ser cuadrada.

Ejemplo:

Matriz Aumentada

Esta matriz contiene, en cada una de las primeras columnas, los coeficientes correspondientes a una variable del sistema de ecuaciones y la última columna contiene el lado derecho de las ecuaciones.

 Ejemplo: